コード・トライアスロン２の解答と第一問の解き方

CodeIQにて、Kawazoeさん（@riverplus）の問題「コード・トライアスロン２」を解きました。解答は記事の最下部に示します。本記事では、特に第一問の解き方を書いておきます。

■問題概要

四角形ABCDについて、∠ABD＝a，∠CBD＝b，∠ACB＝c，∠ACD＝dとおいたとき、∠ADBを10⁶倍したものの整数部分F(a，b，c，d)を求める。
自然数nに対し、次の性質をもつ自然数dの総和をG(n)と定義する。
「nをdで割った余りが1に等しい」
1の結果を受け取り、G(F(a，b，c，d))を求める。
先頭にゼロを持たない自然数であって、逆から読んでも同じ数になる数を回文数という（例：1，22，343，440044，7890987）。自然数mに対し、m以下の回文数の総和をH(m)と定義する。2の結果を受け取り、H(G(F(a，b，c，d)))を求める。

■第一問の解き方

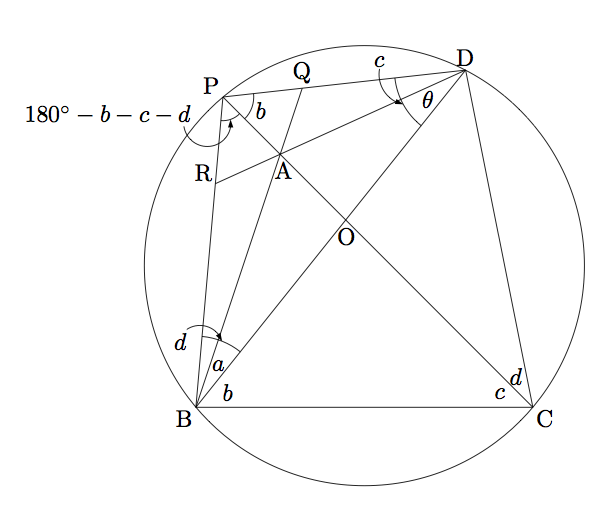
四角形ABCDの対角線の交点をOとする。
四角形ABCDの点B,C,Dを通る円を描き、
四角形ABCDの対角線ACの延長との交点をPとする。
また、PDとABの延長との交点をQ、PBとADの延長との交点をRとする。
∠ABD＝a, ∠CBD＝b,∠ACB＝c,∠ACD＝dより、
弧CDの円周角なので∠CPD＝∠CBD＝b、
弧BPの円周角なので∠BDP＝∠BCP＝∠ACB＝c、
弧DPの円周角なので∠DBP＝∠DCP＝∠ACD＝dとなる。
また、三角形PBCの内角の和を180°なので、
∠BPC＝180°−b−c−dとなる。
三角形PBDにおいてチェバの定理より

\(
\begin{eqnarray}
&&\frac{\hbox{BO}}{\hbox{OD}}\cdot\frac{\hbox{DQ}}{\hbox{QP}}\cdot\frac{\hbox{PR}}{\hbox{RB}}=1\\
&\Leftrightarrow&\frac{\bigtriangleup\hbox{PBO}}{\bigtriangleup\hbox{POD}}\cdot
\frac{\bigtriangleup\hbox{BDQ}}{\bigtriangleup\hbox{BQP}}\cdot
\frac{\bigtriangleup\hbox{DPR}}{\bigtriangleup\hbox{DRB}}=1\\
&\Leftrightarrow&\frac{\frac{1}{2}\cdot\hbox{PB}\cdot\hbox{PO}\cdot\sin\angle\hbox{OPB}}
{\frac{1}{2}\cdot\hbox{PD}\cdot\hbox{PO}\cdot\sin\angle\hbox{OPD}}\cdot
\frac{\frac{1}{2}\cdot\hbox{BD}\cdot\hbox{BQ}\cdot\sin\angle\hbox{QBD}}
{\frac{1}{2}\cdot\hbox{BP}\cdot\hbox{BQ}\cdot\sin\angle\hbox{QBP}}\cdot
\frac{\frac{1}{2}\cdot\hbox{DP}\cdot\hbox{DR}\cdot\sin\angle\hbox{RDP}}
{\frac{1}{2}\cdot\hbox{DB}\cdot\hbox{DR}\cdot\sin\angle\hbox{RDB}}=1\\
&\Leftrightarrow&\frac{\sin\angle\hbox{OPB}}{\sin\angle\hbox{OPD}}\cdot
\frac{\sin\angle\hbox{QBD}}{\sin\angle\hbox{QBP}}\cdot
\frac{\sin\angle\hbox{RDP}}{\sin\angle\hbox{RDB}}=1\\
&\Leftrightarrow&\frac{\sin(180^\circ-b-c-d)}{\sin b}\cdot
\frac{\sin a}{\sin(d-a)}\cdot
\frac{\sin(c-\theta)}{\sin\theta}=1\\
&\Leftrightarrow&\frac{\sin(b+c+d)}{\sin b}\cdot
\frac{\sin a}{\sin(d-a)}\cdot
\frac{\sin c \cos \theta – \cos c \sin \theta}{\sin\theta}=1\\
&\Leftrightarrow&\frac{\sin c \cos \theta – \cos c \sin \theta}{\sin\theta}=
\frac{\sin b \sin(d-a)}{\sin(b+c+d)\sin a}\\
&\Leftrightarrow&\frac{\sin c}{\tan\theta}-\cos c=\frac{\sin b \sin (d-a)}{\sin(b+c+d)\sin a}\\
&\Leftrightarrow&\sin c-\cos c \tan\theta=\frac{\sin b \sin(d-a)}{\sin(b+c+d)\sin a}\cdot\tan\theta\\
&\Leftrightarrow&\left(\frac{\sin b \sin(d-a)}{\sin(b+c+d)\sin a}+\cos c \right)\cdot\tan\theta=\sin c\\
&\Leftrightarrow&\tan\theta=\frac{\sin c}{\frac{\sin b \sin(d-a)}{\sin(b+c+d)\sin a}+\cos c}\\
&\Leftrightarrow&\tan \theta=\frac{\sin(b+c+d)\sin a \sin c}{\sin b \sin(d-a)+\sin(b+c+d)\sin a \cos c}
\end{eqnarray}
\)

θの10⁶を求めるようC++で書くと以下のようになります。

double f = atan((sin((b + c + d) * M_PI / 180) * sin(a * M_PI / 180) *
		 sin(c * M_PI / 180)) /
		(sin(b * M_PI / 180) * sin((d - a) * M_PI / 180) +
		 sin((b + c + d) * M_PI / 180) * sin(a * M_PI / 180) *
		 cos(c * M_PI / 180))) * 180000000 / M_PI;

if(f < 0) {
  f += 180000000;
}

■解答

あまり綺麗なコードではないですが、C++で書いた解答を以下に示します。

#include <iostream>
#include <iterator>
#include <string>
#include <vector>
#include <sstream>
#include <math.h>
#include <stdlib.h>

#define _USE_MATH_DEFINES

using namespace std;

vector<string> split(const string &str){
  istringstream iss(str);
  vector<string> res;
  
  copy(istream_iterator<string>(iss), istream_iterator<string>(),
       back_inserter(res));
  
  return res;
}

struct hResult {
public:
  vector<string> cache;
  long long result;
  hResult() {
    result = 0;
  }
};

hResult h(int size, int limit) {
  int limitSize = to_string(limit).size();

  if(size == 1) {
    hResult result;
    int j = 0;
    
    for(int i = (size == limitSize) ? 1 : 0; i <= 9; i++) {
      if(i <= limit) {
	result.result += i;
	result.cache.push_back(to_string(i));
      } else {
	break;
      }
    }

    return result;
  } else if(size == 2) {
    hResult currentResult, result;
    int j = 0;
    
    if(limitSize == 2) {
      result = h(1, limit);
    }
    
    for(int i = (size == limitSize) ? 1 : 0; i <= 9; i++) {
      string numStr = to_string(i) + to_string(i);
      int numInt = stoi(numStr);
      
      if(numInt <= limit) {
	currentResult.result += numInt;
	currentResult.cache.push_back(numStr);
      } else {
	break;
      }
    }

    if(limitSize == 2) {
      currentResult.result += result.result;
    }

    return currentResult;
  } else {
    hResult result = h(size - 2, limit);
    hResult currentResult;
    int cacheSize = result.cache.size();

    currentResult.result += result.result;

    if(size == limitSize) {
      currentResult.result += h(size - 1, limit).result;
    }

    for(int i = (size == limitSize) ? 1 : 0; i <= 9; i++) {
      for(int j = 0; j < cacheSize; j++) {
	string numStr = to_string(i) + result.cache[j] + to_string(i);
	int numInt = 0;
	
	if(i != 0) {
	  numInt = stoi(numStr);
	}  
	
	if(numInt <= limit) {
	  currentResult.result += numInt;
	  currentResult.cache.push_back(numStr);
	} else {
	  i = 10;
	  break;
	}
      }
    }
    
    return currentResult;
  }
}

int main() {  
  string line;
  int a, b, c, d = 0;
  
  for(; getline(cin, line); ) {
    vector<string> tmp = split(line);

    a = stoi(tmp[0]);
    b = stoi(tmp[1]);
    c = stoi(tmp[2]);
    d = stoi(tmp[3]);
  }

  double f = atan((sin((b + c + d) * M_PI / 180) * sin(a * M_PI / 180) *
		   sin(c * M_PI / 180)) /
		  (sin(b * M_PI / 180) * sin((d - a) * M_PI / 180) +
		   sin((b + c + d) * M_PI / 180) * sin(a * M_PI / 180) *
		   cos(c * M_PI / 180))) * 180000000 / M_PI;
  
  if(f < 0) {
    f += 180000000;
  }
  
  int F = stoi(to_string(f));
  int G = 0;
  
  for(int i = 1; i < F; i++) {
    if(F % i == 1) {
      G += i;
    }
  }
  
  hResult H = h(to_string(G).size(), G);
  
  cout<<H.result<<endl;
}

参考：
ラングレーの問題、整角四角形
 チェバの定理・メネラウスの定理
 PickUp問題②：ラングレーの問題における三角関数の扱い方
 C++で文字列のsplit | Story of Your Life

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル